语义搜索效果差？试试重排

前段时间我开发了一个用白话文搜索语义相近的古诗词的应用（详见： 如何假装文艺青年，怎么把大白话“变成”古诗词？），但是有时候搜索结果却不让人满意，排名靠前的结果和查询的语义没啥关系，靠后的结果反而和查询更相似。比如，我用白话文“今天的雨好大”搜索，前三个结果是：

今日云景好，水绿秋山明。
今日风日好，明日恐不如。
雨落不上天，水覆难再收。

前两个都和雨没有关系，第三个勉强沾边。

为啥语义更相近的句子，反而排名靠后呢？主要有两个原因，一个是“不理解”，另一个是“难精确”。

“不理解”和嵌入模型有关。我使用的嵌入模型可能训练语料中古诗词较少，导致它不能很好地“理解”古诗词的语义。

“难精确”指的是不论你的度量方法使用的是余弦相似度（Cosine），还是欧几里得距离（L2），都不能保证语义最相似的结果一定排在第一。这些方法都是简化的模型，句子的语义内涵很难只用中学数学知识就能准确计算，只能说在整体趋势上，得分越高的结果语义和查询越接近。这就好像深圳入冬后，我们预测温度在10-20°C 之间，这样的预测整体来说是正确的，但是具体到每一天的温度就不一定准确了，可能有那么一两天，温度升到了25°C。

这样的预测相当于语义搜索中的初步搜索，叫做“粗排”。想要优化搜索结果，重新排名，还需要“重排”，也就是 rerank。

除此之外，还有一种情况下也需要重排，那就是混合搜索。我在 门外汉如何“冒充”专家？向量嵌入之稀疏向量 这篇文章中介绍了稀疏向量，稠密向量和稀疏向量各有优势，怎么各取所长呢？可以先分别搜索（也就是混合搜索），再用搜索结果综合起来，而重排就是一种综合多种搜索结果的方法。

这两种重排有所区别，第一种是基于深度学习的重排，第二种是基于统计的重排。第二种原理更简单，我们先来了解第二种。[1]

本文首发于 Zilliz 公众号。文中代码的 Notebook 在这里下载。

基于统计的重排

基于统计的重排用于混合搜索，它可以把多种搜索结果综合起来，重新排序。除了前面介绍的稠密向量和稀疏向量，还可以综合文本向量和图片向量。

怎么综合呢？有两种方法，一种是 WeightedRanker ——分数加权平均算法，通过设置权重计算得分，后面简称权重策略。另一种是 RRFRanker（Reciprocal Rank Fusion）——逆序排名融合算法，通过排名的倒数来计算得分，后面简称 RRF 策略。

权重策略

权重策略就是设置权重。权重值范围从0到1，数值越大表示重要性越大。计算方法很简单，初始得分乘以权重，就是最终得分。[2]

$$\text{WeightedRanker_score} = \sum_{i=1}^{N} (w_i \times \text{score_n}_i) $$

打个比方，假设某班级考了语文和数学两门课，统计出学生每门科目的分数和排名。学生就相当于向量数据库中的文档，学生这两门课的分数，就相当于文档在不同搜索结果中的得分。

假设学生的成绩如下表所示：

学生编号 数学成绩 语文成绩
S1 100 50
S2 95 55
S3 80 70
S4 65 85
S5 80 75
S6 75 80
S7 70 85
S8 65 80
S9 60 85
S10 55 95

在权重策略下，综合得分公式为：
$$score = 数学成绩 * 0.7 + 语文成绩 * 0.3$$
根据公式计算出学生们的综合分数，排名如下：

权重综合排名 权重综合得分 学生编号 数学成绩 语文成绩
1 85 S1 100 50
2 83 S2 95 55
3 78.5 S5 80 75
4 77 S3 80 70
5 76.5 S6 75 80
6 74.5 S7 70 85
7 71 S4 65 85
8 69.5 S8 65 80
9 67.5 S9 60 85
10 67 S10 55 95

RRF 策略

RRF 策略的计算方式稍微复杂一点：
$$\text{RRF_score}(d) = \sum_{i=1}^{N} \frac{1}{k + \text{rank}_i (d)}$$

公式中的 rank 是初始分数的排名，k 是平滑参数。从公式中可以看出，排名越靠前，rank 的值越小，综合得分越高。同时， k 的值越大，排名对分数的影响越小。

我们使用 RRF 策略重新计算分数和排名。参数 k 一般为60，为方便演示，这里设为 10，公式变成：
$$\text{RRF_score}(d) = \sum_{i=1}^{N} \frac{1}{10 + \text{rank}_i (d)}$$

RRF 策略根据排名计算分数，所以我们先列出数学和语文的排名。
数学成绩排名：

数学排名 数学成绩 学生编号
1 100 S1
2 95 S2
3 80 S3
3 80 S5
5 75 S6
6 70 S7
7 65 S8
7 65 S4
9 60 S9
10 55 S10

语文成绩排名：

语文排名 语文成绩 学生编号
1 95 S10
2 85 S4
2 85 S7
2 85 S9
5 80 S6
5 80 S8
7 75 S5
8 70 S3
9 55 S2
10 50 S1

接下来使用 RRF 策略计算综合得分，重新排名：

RRF 综合排名 RRF 综合得分 学生编号 数学成绩 语文成绩
1 0.1458 S7 70 85
2 0.1421 S4 65 85
3 0.1409 S1 100 50
3 0.1409 S10 55 95
5 0.1359 S2 95 55
5 0.1359 S9 60 85
7 0.1357 S5 80 75
8 0.1334 S6 75 80
9 0.1325 S3 80 70
10 0.1255 S8 65 80

比较两个排名可以发现，在权重策略下，数学的权重较大，偏科学生 S1虽然语文只有50分，也能因为数学100分而排在第一名。而 RRF 策略注重的是各科的排名，而不是分数，所以 S1的数学虽然排名第一，但是语文排名第10，综合排名下降到第三。

学生 S7 正好相反，在权重策略下，即使他语文得了85的高分，但是权重只占30%，而高权重的数学只得了70分，所以综合排名靠后，排在第六名。在 RRF 策略下，他的数学和语文排名分别是第六名和第二名，语文的高排名拉高了综合排名，上升到了第一名。

通过比较两种策略的排名结果，我们发现了这样的规律，如果你更看重搜索结果的得分，就使用权重策略，你还可以通过调整权重来调整得分；如果你更看重搜索结果的排名，就使用RRF策略。

基于深度学习的重排

和基于统计的重排相比，基于深度学习的重排更加复杂，通常被称为 Cross-encoder Reranker，交叉编码重排，后面简称“重排模型”。

粗排和重排模型有什么区别呢？粗排搜索速度更快，重排模型准确性更高。

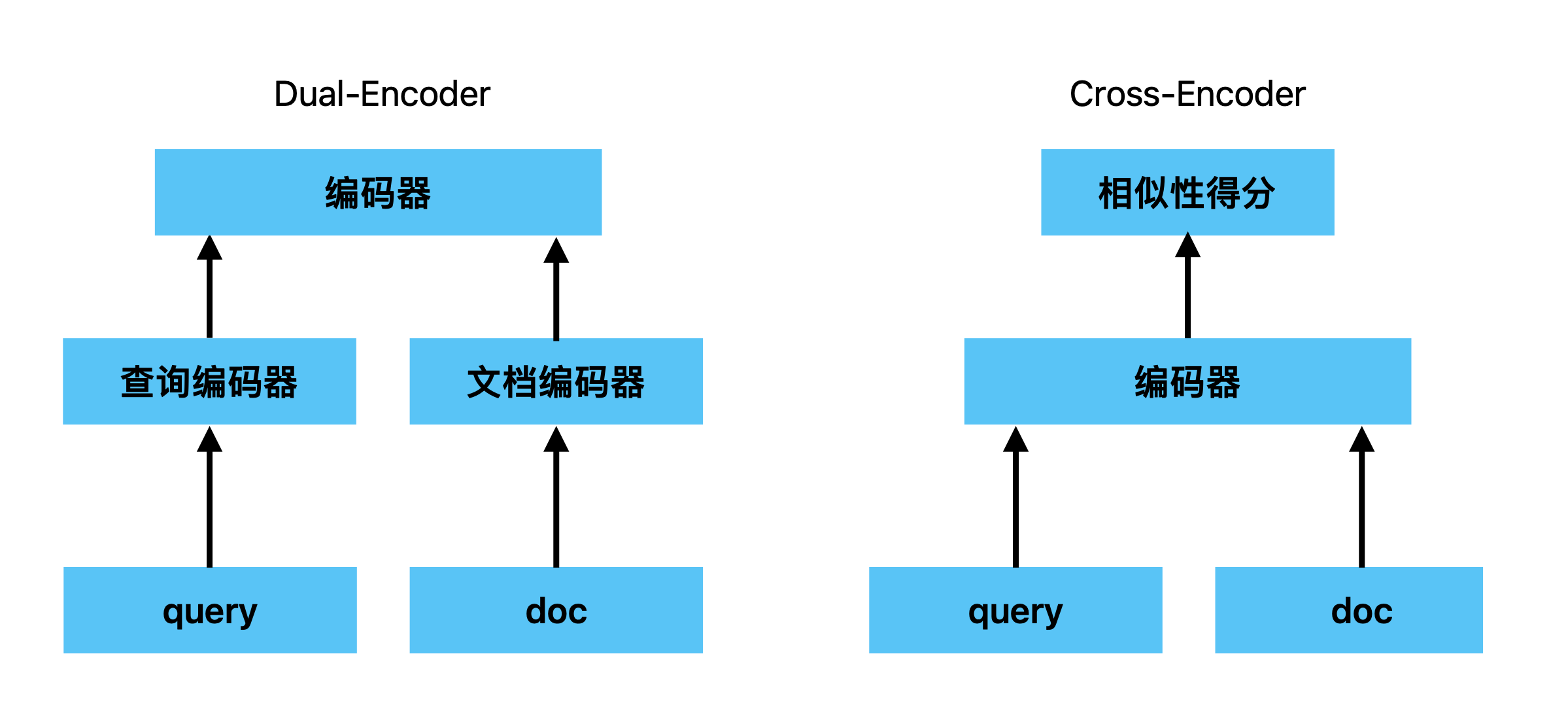
为什么粗排搜索速快？粗排使用的是双塔模型（Dual-Encoder），“双塔”指的是它有两个独立的编码器，分别把查询和文档向量化，然后通过计算向量之间的相似度（比如余弦相似度Cosine）搜索结果并且排序。双塔模型的优势在于搜索效率高，因为可以提前计算文档向量，搜索时只需要向量化查询即可。而重排模型则是在搜索时现场编码。就好比两个饭店，一个使用预制菜，一个现场热炒，上菜速度肯定不一样。

重排模型的优势则是准确性高。它把查询和文档组成数据对后输入给编码器编码，然后给它们的相似程度打分，针对性强。这就相当于公司招聘人才，粗排是根据专业、学历和工作年限等几个指标快速筛选简历，挑选出多位候选者。重排则是通过面试详细了解候选者做过什么项目，遇到了什么挑战，解决了什么难题，然后判断他有多适合应聘的岗位（文档与查询有多相似）。

image.png|600
图片来源：自己画的

所以，重排模型适合那些对回答准确性要求高的场景，比如专业知识库或者客服系统。不适合追求高响应速度和低成本的场景，比如网页搜索、电商，这种场景建议使用基于统计的重排。

你还可以把粗排和重排模型结合起来。比如，先通过粗排筛选出10个候选结果，再用重排模型重新排名。既可以提高搜索速度，也能保证准确度。

代码实践

版本说明：
Milvus 版本：>=2.5.0
pymilvus 版本：>=2.5.0

接下来我们通过代码实践一下，看看这些重排方法实际效果到底如何。

我们会使用“敏捷的狐狸跳过懒惰的狗。”作为查询，从下面10个句子中搜索出语义相似的句子。你可以先猜一猜，粗排、基于统计的重排以及基于深度学习的重排，哪个效果最好。

文档：

1
2
3
4
5
6
7
8
9
10
11
12
13
[
	{"content": "灵活的狐跳过了懒散的犬。"},
	{"content": "一只敏捷的狐在公园里跳过了那只懒犬。"},
	{"content": "那只懈怠的犬正在大树下睡觉。"},
	{"content": "在公园里，那只棕色的狐狸正在跳。"},
	{"content": "犬跃过了狐。"},
	{"content": "树下有一个小池塘。"},
	{"content": "动物如狗和狐狸生活在公园里。"},
	{"content": "池塘靠近公园里的大树。"},
	{"content": "懒狗跳过了狐狸。"},
	{"content": "那只灵巧的狐狸轻松地跨过了那只懒散的狗。"},
	{"content": "狐迅速地跳过了那只不活跃的犬。"}
]

首先创建集合。我们为集合设置稠密向量“dense_vectors”和稀疏向量“sparse_vectors”两个字段，分别储存稠密向量和稀疏向量，用于混合搜索。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
from pymilvus import MilvusClient, DataType
import time

# 检查并且删除同名集合
def check_and_drop_collection(collection_name):
    if milvus_client.has_collection(collection_name):
        print(f"集合 {collection_name} 已经存在")
        try:
            milvus_client.drop_collection(collection_name)
            print(f"删除集合：{collection_name}")
            return True
        except Exception as e:
            print(f"删除集合时出现错误: {e}")
            return False
    return True


# 创建模式
def create_schema():
    schema = milvus_client.create_schema(
        auto_id=True,
        enable_dynamic_field=True,
        description=""
    )
    schema.add_field(field_name="id", datatype=DataType.INT64, is_primary=True, max_length=256)
    schema.add_field(field_name="content", datatype=DataType.VARCHAR, max_length=256)
    schema.add_field(field_name="dense_vectors", datatype=DataType.FLOAT_VECTOR, dim=1024)
    schema.add_field(field_name="sparse_vectors", datatype=DataType.SPARSE_FLOAT_VECTOR)
    return schema


# 创建集合
import time
def create_collection(collection_name, schema, timeout = 3):
    # 创建集合
    try:
        milvus_client.create_collection(
            collection_name=collection_name,
            schema=schema,
            shards_num=2
        )
        print(f"开始创建集合：{collection_name}")
    except Exception as e:
        print(f"创建集合的过程中出现了错误: {e}")
        return False

    # 检查集合是否创建成功
    start_time = time.time()
    while True:
        if milvus_client.has_collection(collection_name):
            print(f"集合 {collection_name} 创建成功")
            return True
        elif time.time() - start_time > timeout:
            print(f"创建集合 {collection_name} 超时")
            return False
        time.sleep(1)

class CollectionDeletionError(Exception):
    """删除集合失败"""



collection_name = "test_rank"
uri="http://localhost:19530"
milvus_client = MilvusClient(uri=uri)

# 如果无法删除集合，抛出异常
if not check_and_drop_collection(collection_name):
    raise CollectionDeletionError('删除集合失败')
else:
    # 创建集合的模式
    schema = create_schema()
    # 创建集合并等待成功
    create_collection(collection_name, schema)

然后，定义把文档向量化的函数。我们使用 bge_m3 生成稠密向量和稀疏向量。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
from tqdm import tqdm
import torch
from pymilvus.model.hybrid import BGEM3EmbeddingFunction

# 初始化嵌入模型的实例
def init_embedding_model():
    # 检查是否有可用的CUDA设备
    device = "cuda:0" if torch.cuda.is_available() else "cpu"
    # 根据设备选择是否使用fp16
    use_fp16 = device.startswith("cuda")
    # 创建嵌入模型实例
    bge_m3_ef = BGEM3EmbeddingFunction(
        model_name="BAAI/bge-m3",
        device=device,
        use_fp16=use_fp16
    )
    return bge_m3_ef


# 把查询向量化
def vectorize_query(query, encoder):
    # 验证参数是否符合要求
    if not (isinstance(query, list) and all(isinstance(text, str) for text in query)):
        raise ValueError("query必须为字符串列表。")
    return encoder.encode_queries(query)


# 把文档向量化
def vectorize_docs(docs, encoder):
    # 验证参数是否符合要求
    if not (isinstance(docs, list) and all(isinstance(text, str) for text in docs)):
        raise ValueError("docs必须为字符串列表。")
    return encoder.encode_documents(docs)


# 初始化嵌入模型实例
bge_m3_ef = init_embedding_model()

接下来，生成向量并且导入向量数据库。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
import json

# 把文件中的指定字段向量化
def vectorize_file(input_file_path, encoder, field_name):
    with open(input_file_path, 'r', encoding='utf-8') as file:
        data_list = json.load(file)
        docs = [data[field_name] for data in data_list]
    # 向量化文档
    return vectorize_docs(docs, encoder), data_list


# 把数据插入数据库
def insert_data(
    collection_name: str,
    data_list,
    dense_vectors,
    sparse_vectors,
    batch_size: int = 1000):
    # 定义默认稀疏向量，避免生成稀疏向量失败。元素值全为0，表示它在所有维度上都不重要
    default_sparse_vector = {0: 1.0, 1: 1.0, 2: 1.0, 3: 1.0}

    # 接收稠密向量和稀疏向量
    for data, dense_vector, sparse_vector in zip(data_list, dense_vectors, sparse_vectors):
        data['dense_vectors'] = dense_vector
        # 如果稀疏向量为空，则使用默认稀疏向量，避免入库时报错
        if sparse_vector is not None:
            data['sparse_vectors'] = sparse_vector
        else:
            data['sparse_vectors'] = default_sparse_vector

    # 分批入库
    print(f"正在将数据插入集合：{collection_name}")
    total_count = len(data_list)
    with tqdm(total=total_count, desc="插入数据") as progress_bar:
        # 每次插入 batch_size 条数据
        for i in range(0, total_count, batch_size):  
            batch_data = data_list[i:i + batch_size]
            res = milvus_client.insert(
                collection_name=collection_name,
                data=batch_data
            )
            progress_bar.update(len(batch_data))


input_file_path = "docs_rank.json"
field_name = "content"
vectors, data_list = vectorize_file(input_file_path, bge_m3_ef, field_name)
docs_dense_vectors = vectors['dense']
docs_sparse_vectors = vectors['sparse']
insert_data(collection_name, data_list, docs_dense_vectors, docs_sparse_vectors)

数据入库后，为它们创建索引。因为数据库中同时包含了两个向量，所以使用混合搜索，需要分别创建稠密向量和稀疏向量的索引。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
index_params = milvus_client.prepare_index_params()

# 创建密集向量索引参数
index_params.add_index(
    index_name="IVF_FLAT",
    field_name="dense_vectors",
    index_type="IVF_FLAT",
    metric_type="COSINE",
    params={"nlist": 128}
)

# 创建稀疏向量索引参数
index_params.add_index(
    index_name="sparse",
    field_name="sparse_vectors",
    index_type="SPARSE_INVERTED_INDEX",
    # 目前仅支持IP
    metric_type="IP",
    params={"drop_ratio_build": 0.2}
)

加载集合。

1
2
3
4
5
print(f"正在加载集合：{collection_name}")
milvus_client.load_collection(collection_name=collection_name)

# 验证加载状态
print(milvus_client.get_load_state(collection_name=collection_name))

为了实现混合搜索，还需要定义混合搜索函数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
# 混合搜索
from pymilvus import AnnSearchRequest, WeightedRanker, RRFRanker

def perform_hybrid_search(
    collection_name, 
    query, 
    ranker,
    output_fields,
    limit_dense,
    limit_sparse,
    limit_hybrid
    ):
    # 获取查询的稠密向量和稀疏向量
    query_vectors = vectorize_query(query, bge_m3_ef)
    query_dense_vectors = [query_vectors['dense'][0]]
    query_sparse_vectors = [query_vectors['sparse'][[0]]]
    # 创建稠密向量的搜索参数
    dense_search_params = {
        # 查询向量
        "data": query_dense_vectors,  
        "anns_field": "dense_vectors",
        "param": {
            "metric_type": "COSINE",
            "params": {
                "nprobe": 16,
                "radius": 0.1,
                "range_filter": 1
            }
        },
        "limit": limit_dense
    }
    # 创建稠密向量的搜索请求
    dense_req = AnnSearchRequest(**dense_search_params)
    
    # 创建稀疏向量的搜索参数
    sparse_search_params = {
        "data": query_sparse_vectors,
        "anns_field": "sparse_vectors",
        "param": {
            "metric_type": "IP",
            "params": {"drop_ratio_search": 0.2}
        },
        "limit": limit_sparse
    }
    # 创建稀疏向量的搜索请求
    sparse_req = AnnSearchRequest(**sparse_search_params)
    # 执行混合搜索
    start_time = time.time()
    res = milvus_client.hybrid_search(
        collection_name=collection_name,
        reqs=[dense_req, sparse_req],
        ranker = ranker,
        limit=limit_hybrid,
        output_fields=output_fields
    )
    end_time = time.time()
    total_time = end_time - start_time
    print(f"搜索时间：{total_time:.3f}")
    return res

最后再定义一个打印函数，方便查看搜索结果。

1
2
3
4
5
6
7
8
def print_vector_results(res):   
    for hits in res:
        for hit in hits:
            entity = hit.get("entity")
            print(f"content: {entity['content']}")
            print(f"distance: {hit['distance']:.4f}")
            print("-"*50)
        print(f"数量：{len(hits)}")

对比搜索结果

准备工作就绪，先分别看下稠密向量和稀疏向量的搜索结果。在混合搜索的权重策略下，调整权重，一个设置1，另一个设置为0，就可以只查看一种搜索结果。

1
2
3
4
5
6
7
8
9
query = ["敏捷的狐狸跳过懒惰的狗。"]
ranker=WeightedRanker(1, 0)
output_fields = ["content"]
limit_dense = 10
limit_sparse = 10
limit_hybrid = 10

res_dense = perform_hybrid_search(collection_name, query, ranker, output_fields, limit_dense, limit_sparse, limit_hybrid)
print_vector_results(res_dense)

稠密向量的搜索结果勉强及格，正确答案分别排在第一、第三、第四和第五。让人不满意的是，语义和查询完全相反的句子，却排在了第二和第六，而且前6个搜索结果的得分相差很小，区别不明显。

另外，留意一下搜索时间是0.012秒，后面要和基于深度学习的重排做比较。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
搜索时间：0.012
content: 灵活的狐跳过了懒散的犬。
distance: 0.9552
--------------------------------------------------
content: 懒狗跳过了狐狸。
distance: 0.9444
--------------------------------------------------
content: 一只敏捷的狐在公园里跳过了那只懒犬。
distance: 0.9373
--------------------------------------------------
content: 那只灵巧的狐狸轻松地跨过了那只懒散的狗。
distance: 0.9366
--------------------------------------------------
content: 狐迅速地跳过了那只不活跃的犬。
distance: 0.9194
--------------------------------------------------
content: 犬跃过了狐。
distance: 0.9025
--------------------------------------------------
content: 在公园里，那只棕色的狐狸正在跳。
distance: 0.8456
--------------------------------------------------
content: 动物如狗和狐狸生活在公园里。
distance: 0.8303
--------------------------------------------------
content: 那只懈怠的犬正在大树下睡觉。
distance: 0.7702
--------------------------------------------------
content: 树下有一个小池塘。
distance: 0.7174
--------------------------------------------------
数量：10

调整权重，再来看看稀疏向量的结果。

1
2
3
ranker=WeightedRanker(0, 1)
res_sparse = perform_hybrid_search(collection_name, query, ranker, output_fields, limit_dense, limit_sparse, limit_hybrid)
print_vector_results(res_sparse)

稀疏向量的搜索结果不太理想，第一个搜索结果是正确的，第二、第三个搜索结果和查询相差太大，另一个正确答案在第四位才出现。搜索时间是0.014秒，和稠密向量相当。

稀疏向量的搜索结果就更差了，正确答案分别排在第二、第三、第六和第七。这是因为我特意用语义相近但是文本不同的词做了替换，比如用“犬”代替“狗”，“懈怠”代替“懒”，导致它们较难命中查询中的词，得分较低。如果你想了解稀疏向量是如何参与搜索并且计算得分的，可以看看 门外汉如何“冒充”专家？向量嵌入之稀疏向量 这篇文章。

搜索时间是0.014秒，和稠密向量相当。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
搜索时间：0.014
content: 懒狗跳过了狐狸。
distance: 0.5801
--------------------------------------------------
content: 那只灵巧的狐狸轻松地跨过了那只懒散的狗。
distance: 0.5586
--------------------------------------------------
content: 一只敏捷的狐在公园里跳过了那只懒犬。
distance: 0.5553
--------------------------------------------------
content: 在公园里，那只棕色的狐狸正在跳。
distance: 0.5502
--------------------------------------------------
content: 动物如狗和狐狸生活在公园里。
distance: 0.5476
--------------------------------------------------
content: 灵活的狐跳过了懒散的犬。
distance: 0.5441
--------------------------------------------------
content: 狐迅速地跳过了那只不活跃的犬。
distance: 0.5336
--------------------------------------------------
content: 犬跃过了狐。
distance: 0.5192
--------------------------------------------------
content: 那只懈怠的犬正在大树下睡觉。
distance: 0.5006
--------------------------------------------------
content: 树下有一个小池塘。
distance: 0.0000
--------------------------------------------------
数量：10

接下来是重点了，我们分别使用权重策略和 RRF 策略，看看重排后的结果如何。

先来看看权重策略中，权重是如何影响综合得分的。我们给稠密向量设置更高的权重——0.8，稀疏向量的权重则设置为0.2。

1
2
3
ranker=WeightedRanker(0.8, 0.2)
res_Weighted = perform_hybrid_search(collection_name, query, ranker, output_fields, limit_dense, limit_sparse, limit_hybrid)
print_vector_results(res_Weighted)

综合排名第一的结果“灵活的狐跳过了懒散的犬。”，在稠密向量中的得分是0.9552，排名也是第一，与第二名相差0.108。

它在稀疏向量中的得分是0.5441，排名第六。虽然排名低，但是得分与第一名只差0.036分，而且权重只占0.2，对综合得分仍然是第一。因为稠密向量的权重高，综合排名基本和稠密向量的排名一致。

搜索时间是0.022秒。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
搜索时间：0.022
content: 灵活的狐跳过了懒散的犬。
distance: 0.8730
--------------------------------------------------
content: 懒狗跳过了狐狸。
distance: 0.8716
--------------------------------------------------
content: 那只灵巧的狐狸轻松地跨过了那只懒散的狗。
distance: 0.8610
--------------------------------------------------
content: 一只敏捷的狐在公园里跳过了那只懒犬。
distance: 0.8609
--------------------------------------------------
content: 狐迅速地跳过了那只不活跃的犬。
distance: 0.8423
--------------------------------------------------
content: 犬跃过了狐。
distance: 0.8259
--------------------------------------------------
content: 在公园里，那只棕色的狐狸正在跳。
distance: 0.7865
--------------------------------------------------
content: 动物如狗和狐狸生活在公园里。
distance: 0.7738
--------------------------------------------------
content: 那只懈怠的犬正在大树下睡觉。
distance: 0.7163
--------------------------------------------------
content: 树下有一个小池塘。
distance: 0.5739
--------------------------------------------------
数量：10

接下来，我们来看看权重策略下的第一名，在 RRF 策略中表现如何。

1
2
3
ranker = RRFRanker(k=10)
res_rrf = perform_hybrid_search(collection_name, query, ranker, output_fields, limit_dense, limit_sparse, limit_hybrid)
print_vector_results(res_rrf)

“灵活的狐跳过了懒散的犬。”在 RRF 策略中的排名从第一下滑到了第四。因为这次注重的是排名，它在稠密向量中虽然排名第一，但是在稀疏向量中的排名只有第六，拉低了综合排名。

排名第一是“懒狗跳过了狐狸。”，因为它在两个搜索结果中的排名都很高，分别是第二和第一。

搜索时间是0.022秒，和权重策略的搜索时间差不多。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
搜索时间：0.022
content: 懒狗跳过了狐狸。
distance: 0.1742
--------------------------------------------------
content: 那只灵巧的狐狸轻松地跨过了那只懒散的狗。
distance: 0.1548
--------------------------------------------------
content: 一只敏捷的狐在公园里跳过了那只懒犬。
distance: 0.1538
--------------------------------------------------
content: 灵活的狐跳过了懒散的犬。
distance: 0.1534
--------------------------------------------------
content: 在公园里，那只棕色的狐狸正在跳。
distance: 0.1303
--------------------------------------------------
content: 狐迅速地跳过了那只不活跃的犬。
distance: 0.1255
--------------------------------------------------
content: 动物如狗和狐狸生活在公园里。
distance: 0.1222
--------------------------------------------------
content: 犬跃过了狐。
distance: 0.1181
--------------------------------------------------
content: 那只懈怠的犬正在大树下睡觉。
distance: 0.1053
--------------------------------------------------
content: 树下有一个小池塘。
distance: 0.0500
--------------------------------------------------
数量：10

终于，轮到我们最期待的重排模型上场了。其实，因为返回的搜索结果数量和文档中的句子数量相同，对任何一个搜索结果重排，或者直接对文档重排，效果都是一样的。不过，为了和实际应用中的粗排、重排流程一致，我们还是对粗排结果重排，比如稀疏向量的搜索结果。

首先，我们要以字符串列表的形式，获取稀疏向量的搜索结果，以满足重排模型的输入要求。

1
2
3
4
5
6
7
8
9
10
11
# 获取稀疏向量的搜索结果
def get_init_res_list(res, field_name):
    res_list = []
    for hits in res:
        for hit in hits:
            entity = hit.get("entity")
            res_list.append(entity[field_name])
    return res_list

# 为了显示重排的效果，我们对搜索结果最差的稀疏向量做重排
init_res_list = get_init_res_list(res_sparse, field_name)

接下来，定义重排模型。这里使用的是 bge_m3的重排模型。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
from pymilvus.model.reranker import BGERerankFunction

# 定义重排函数
bge_rf = BGERerankFunction(
    model_name="BAAI/bge-reranker-v2-m3",
    device="cpu"
)

def perform_reranking(query: str, documents: list, top_k: int = 10) -> list:
    # 获取重排结果
    start_time = time.time()
    rerank_res = bge_rf(
        # query参数是字符串
        query=query[0],
        # documents参数是字符串列表
        documents=documents,
        top_k=top_k,
    )
    end_time = time.time()
    total_time = end_time - start_time
    print(f"搜索时间：{total_time:.3f}")
    
    return rerank_res

top_k = 10
rerank_res = perform_reranking(query, init_res_list, top_k)

前面我提到过重排模型会花更多的时间，我们先对比下时间。第一次使用重排模型花了3.2秒，后面再使用一般用时0.4秒，这可能是因为第一次需要加载重排模型到内存中，花的时间较多。所以我们按照用时0.4秒计算。

基于统计的重排用时在0.014-0.022秒之间，按照最慢的0.022秒计算。两者时间相差18倍。

重排模型多花了这么多时间，效果怎么样呢？打印搜索结果看看吧。

1
2
3
4
for hit in rerank_res:
    print(f"content: {hit.text}")
    print(f"score: {hit.score:.4f}")
    print("-"*50)

我对重排结果还是比较满意的。四个正确答案排在前四名，而且得分非常接近满分1分。而且，它们和其他搜索结果在得分上终于拉开了较大的差距。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
content: 灵活的狐跳过了懒散的犬。
score: 0.9998
--------------------------------------------------
content: 狐迅速地跳过了那只不活跃的犬。
score: 0.9997
--------------------------------------------------
content: 那只灵巧的狐狸轻松地跨过了那只懒散的狗。
score: 0.9987
--------------------------------------------------
content: 一只敏捷的狐在公园里跳过了那只懒犬。
score: 0.9980
--------------------------------------------------
content: 犬跃过了狐。
score: 0.3730
--------------------------------------------------
content: 懒狗跳过了狐狸。
score: 0.2702
--------------------------------------------------
content: 在公园里，那只棕色的狐狸正在跳。
score: 0.1924
--------------------------------------------------
content: 动物如狗和狐狸生活在公园里。
score: 0.0972
--------------------------------------------------
content: 那只懈怠的犬正在大树下睡觉。
score: 0.0059
--------------------------------------------------
content: 树下有一个小池塘。
score: 0.0000
--------------------------------------------------

总结

通过对比我们发现，基于统计的重排速度快，准确性一般，适合追求高响应速度和低成本的场景，比如网页搜索、电商。

它有权重和 RRF 两个策略。如果你更看重某种类型的搜索结果，建议使用权重策略。如果你没有明显的偏好，希望在不同搜索结果中，排名都靠前的结果能够胜出，建议使用 RRF 策略。

基于深度学习的重排速度慢，但是准确性高，适合对回答准确性要求高的场景，比如专业知识库或者客服系统。

藏宝图

如果你还想了解更多重排的知识，可以参考下面的文章：

参考

  1. 一文玩转 Milvus 新特性之 Hybrid Search ↩
  2. Reranking ↩
向量数据库 > 原理探秘
语义搜索效果差？试试重排
http://example.com/2025/01/15/语义搜索效果差？试试重排/
作者
江浩
发布于
2025年1月15日
许可协议